El mundo de los gráficos 3D puede ser muy intimidante al principio. Ya sea que sólo desee crear un logotipo 3D interactivo o diseñar un juego completo, si no conoces los principios de la representación en 3D, te puedes quedar atrapado en una biblioteca que abstrae un montón de cosas.
Usar una biblioteca puede ser la herramienta adecuada y JavaScript tiene una increíble fuente abierta en forma de three.js. Hay algunas desventajas en el uso de soluciones pre-hechas, aunque:
- Pueden tener muchas características que no planeas utilizar. El tamaño de las características base minificadas tres.js es alrededor de 500kB, y cualquier característica adicional (cargar archivos de modelo real es una de ellas) hacen que la carga útil sea aún más grande. Transferir esa cantidad de datos sólo para mostrar un logotipo giratorio en su sitio web sería un desperdicio.
- Una capa extra de abstracción puede hacer modificaciones que normalmente son fáciles, difíciles de hacer. Su forma creativa de sombrear un objeto en la pantalla puede ser sencilla de implementar o requerir decenas de horas de trabajo para incorporar en las abstracciones de la biblioteca.
- Mientras que la biblioteca se optimiza muy bien en la mayoría de los escenarios, se pueden eliminar adornos extras para tu caso de uso particular. El renderizador puede hacer que ciertos procedimientos se ejecuten millones de veces en la tarjeta gráfica. Cada instrucción eliminada de tal procedimiento significa que una tarjeta gráfica más débil puede manejar tu contenido sin problemas.
Incluso si decides utilizar una biblioteca de gráficos de alto nivel, tener conocimientos básicos de las cosas más escondidas te permite utilizarla con mayor eficacia. Las bibliotecas también pueden tener funciones avanzadas, como ShaderMaterial enthree.js. El conocer los principios de representación gráfica te permite utilizar tales características.

Nuestro objetivo es dar una breve introducción a todos los conceptos clave detrás de la prestación de gráficos 3D y el uso de WebGL para su aplicación. Verás que lo más común que se hace es mostrar y mover objetos 3D en un espacio vacío.
El código final está disponible para que experimentes y juegues con él.
Representando Modelos 3D
Lo primero que tendrías que entender es cómo se representan los modelos 3D. Un modelo está hecho de una malla de triángulos. Cada triángulo está representado por tres vértices para cada una de las esquinas del triángulo. Hay tres propiedades unidas a los vértices que son las más comunes.
Posición del Vértice
La posición es la propiedad más intuitiva de un vértice. Es la posición en el espacio 3D, representada por un vector 3D de coordenadas. Si conoces las coordenadas exactas de tres puntos en el espacio, tendrías toda la información que necesita para dibujar un triángulo simple entre ellos. Para que los modelos parezcan realmente buenos cuando se procesan, hay un par de cosas más que deben proporcionarse al renderizador.
Vértice Normal
Considera los dos modelos anteriores. Consisten en las mismas posiciones del vértice aunque se ven totalmente diferente cuando son representadas. ¿Cómo es eso posible?
Además de decirle al renderer donde queremos que se encuentre un vértice, también podemos darle una pista sobre cómo la superficie está inclinada en esa posición exacta. La pista está en la forma del vector normal de la superficie en ese punto específico del modelo, representado con un vector 3D. La siguiente imagen debe darte un aspecto más descriptivo de cómo se maneja.
Las superficies de la izquierda y derecha corresponden a la bola izquierda y derecha de la imagen anterior, respectivamente. Las flechas rojas representan los vectores normales que se especifican para un vértice, mientras que las flechas azules representan los cálculos del procesador de cómo un vector normal debe buscar todos los puntos entre los vértices. La imagen muestra una demostración para el espacio 2D, pero el mismo principio se aplica en 3D.
El vector normal es un indicio de cómo las luces iluminarán la superficie. Cuanto más cerca está la dirección de un rayo de luz al vector normal, más brillante es el punto. Tener cambios graduales en dirección al vector normal causa gradientes ligeros, mientras que tener cambios abruptos sin cambios entre estos, da como resultado superficies con iluminación constante a través de ellos, al igual que cambios repentinos en la iluminación.
Coordenadas de Textura
La última propiedad significativa son las coordenadas de textura, comúnmente referidas como mapeo UV. Tienes un modelo y una textura que deseas aplicarle. La textura tiene varias áreas y éstas representan las imágenes que queremos aplicar a diferentes partes del modelo. Debe haber una manera de marcar qué triángulo debe representarse con qué parte de la textura. Ahí es donde entra el mapeo de textura.
Para cada vértice, marcamos dos coordenadas, U y V. Estas coordenadas representan una posición en la textura, con U representando el eje horizontal y V el eje vertical. Los valores no están en píxeles sino en una posición porcentual dentro de la imagen. La esquina inferior izquierda de la imagen se representa con dos ceros, mientras que la parte superior derecha se representa con dos unos.
Un triángulo se pinta tomando las coordenadas UV de cada vértice en el triángulo y aplicando la imagen que se captura entre esas coordenadas en la textura.
n modelo OBJ
Lo creas o no, esto es todo lo que necesitas saber para crear tu propio cargador de modelos simple. El formato de archivo OBJ es lo suficientemente simple para implementar un analizador en unas pocas líneas de código.
El archivo enlista las posiciones de los vértices en un formato v <float> <float> <float>, con un cuarto float opcional, que ignoraremos, para mantener las cosas simples. Los vértices se representan de forma similar con vn <float> <float> <float>. Finalmente, las coordenadas de textura se representan con vt <float> <float>, con un tercer float opcional que seguiremos ignorando. En los tres casos, los float representan las respectivas coordenadas. Estas tres propiedades se acumulan en tres matrices.
Los rostros se representan con grupos de vértices. Cada vértice se representa con el índice de cada una de las propiedades, por lo que los índices comienzan en 1. Hay varias maneras de cómo esto está representado, pero nos adheriremos a la ‘v1/vt1/vn1 v2/vt2/vn2 v3/vt3/vn3`, requiriendo que las tres propiedades sean proporcionadas y limitando a tres el número de vértices por cada cara. Todas estas limitaciones se están haciendo para mantener el cargador tan simple como sea posible, ya que todas las demás opciones requieren algún procesamiento extra trivial antes de que puedan estar en un formato que a WebGL le guste.
Hemos puesto muchos requisitos para nuestro cargador de archivos. Eso puede sonar limitante, pero las aplicaciones de modelado 3D tienden a darle la capacidad de establecer esas limitaciones al exportar un modelo como un archivo OBJ.
El siguiente código analiza una cadena que representa un archivo OBJ y crea un modelo en forma de una matriz de rostros.
function Geometry (faces) {
this.faces = faces || []
}
// Parses an OBJ file, passed as a string
Geometry.parseOBJ = function (src) {
var POSITION = /^v\s+([\d\.\+\-eE]+)\s+([\d\.\+\-eE]+)\s+([\d\.\+\-eE]+)/
var NORMAL = /^vn\s+([\d\.\+\-eE]+)\s+([\d\.\+\-eE]+)\s+([\d\.\+\-eE]+)/
var UV = /^vt\s+([\d\.\+\-eE]+)\s+([\d\.\+\-eE]+)/
var FACE = /^f\s+(-?\d+)\/(-?\d+)\/(-?\d+)\s+(-?\d+)\/(-?\d+)\/(-?\d+)\s+(-?\d+)\/(-?\d+)\/(-?\d+)(?:\s+(-?\d+)\/(-?\d+)\/(-?\d+))?/
lines = src.split('\n')
var positions = []
var uvs = []
var normals = []
var faces = []
lines.forEach(function (line) {
// Match each line of the file against various RegEx-es
var result
if ((result = POSITION.exec(line)) != null) {
// Add new vertex position
positions.push(new Vector3(parseFloat(result[1]), parseFloat(result[2]), parseFloat(result[3])))
} else if ((result = NORMAL.exec(line)) != null) {
// Add new vertex normal
normals.push(new Vector3(parseFloat(result[1]), parseFloat(result[2]), parseFloat(result[3])))
} else if ((result = UV.exec(line)) != null) {
// Add new texture mapping point
uvs.push(new Vector2(parseFloat(result[1]), 1 - parseFloat(result[2])))
} else if ((result = FACE.exec(line)) != null) {
// Add new face
var vertices = []
// Create three vertices from the passed one-indexed indices
for (var i = 1; i < 10; i += 3) {
var part = result.slice(i, i + 3)
var position = positions[parseInt(part[0]) - 1]
var uv = uvs[parseInt(part[1]) - 1]
var normal = normals[parseInt(part[2]) - 1]
vertices.push(new Vertex(position, normal, uv))
}
faces.push(new Face(vertices))
}
})
return new Geometry(faces)
}
// Loads an OBJ file from the given URL, and returns it as a promise
Geometry.loadOBJ = function (url) {
return new Promise(function (resolve) {
var xhr = new XMLHttpRequest()
xhr.onreadystatechange = function () {
if (xhr.readyState == XMLHttpRequest.DONE) {
resolve(Geometry.parseOBJ(xhr.responseText))
}
}
xhr.open('GET', url, true)
xhr.send(null)
})
}
function Face (vertices) {
this.vertices = vertices || []
}
function Vertex (position, normal, uv) {
this.position = position || new Vector3()
this.normal = normal || new Vector3()
this.uv = uv || new Vector2()
}
function Vector3 (x, y, z) {
this.x = Number(x) || 0
this.y = Number(y) || 0
this.z = Number(z) || 0
}
function Vector2 (x, y) {
this.x = Number(x) || 0
this.y = Number(y) || 0
}
La estructura Geometry contiene los datos exactos necesarios para enviar un modelo a la tarjeta gráfica para ser procesados. Antes de hacer eso, es probable que quieras tener la capacidad de mover el modelo en la pantalla.
Realización de Transformaciones Espaciales
Todos los puntos en el modelo que cargamos son relativos a su sistema de coordenadas. Si queremos traducir, rotar y escalar el modelo, lo que debemos hacer es realizar esa operación en su sistema de coordenadas. El sistema de coordenadas A, relativo al sistema de coordenadas B, está definido por la posición de su centro como vector p_ab y el vector para cada uno de sus ejes x_ab, y_ab y z_ab, representando la dirección de ese eje. Así que si un punto se mueve por 10 en el eje x del sistema de coordenadas A, entonces — en el sistema de coordenadas B — se moverá en la dirección de x_ab, multiplicado por 10.
Toda esta información se almacena en el siguiente formulario matriz:
x_ab.x y_ab.x z_ab.x p_ab.x
x_ab.y y_ab.y z_ab.y p_ab.y
x_ab.z y_ab.z z_ab.z p_ab.z
0 0 0 1
Si queremos transformar el vector 3D q, sólo tenemos que multiplicar la matriz de transformación con el vector:
q.x
q.y
q.z
1
Esto hace que el punto se mueva por q.x a lo largo del nuevo eje x, por q.y a lo largo del nuevo eje y, y por q.z a lo largo del nuevo eje z. Finalmente hace que el punto se mueva adicionalmente por el vector p, que es la razón por la que usamos un uno como el elemento final de la multiplicación.
La gran ventaja de utilizar estas matrices es el hecho de que si tenemos múltiples transformaciones a realizar en el vértice, podemos fusionarlas en una transformación, multiplicando sus matrices antes de transformar el vértice mismo.
Hay varias transformaciones que se pueden realizar, y echaremos un vistazo a las principales.
Sin Transformación
Si no ocurre ninguna transformación, entonces el vector p es un vector cero, el vector x es [1, 0, 0], y es [0, 1, 0]y z es [0, 0, 1]. A partir de ahora nos referiremos a estos valores como valores por defecto para estos vectores. La aplicación de estos valores nos da una matriz de identidad:
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Éste es un buen punto de partida para encadenar transformaciones.
Traducción
Al momento de realizar la traducción todos los vectores, excepto el vector p, tienen sus valores por defecto. Esto da lugar a la siguiente matriz:
1 0 0 p.x
0 1 0 p.y
0 0 1 p.z
0 0 0 1
Ajuste
Ajustar un modelo significa reducir la cantidad que cada coordenada contribuye a la posición de un punto. No existe un desplazamiento uniforme causado por el ajuste, por lo que el vector p mantiene su valor predeterminado. Los vectores de eje predeterminados deben multiplicarse por sus respectivos factores de escala, lo que da como resultado la siguiente matriz:
s_x 0 0 0
0 s_y 0 0
0 0 s_z 0
0 0 0 1
Aquí s_x, s_y, y s_z representan el ajuste aplicado a cada eje.
Rotación
La imagen anterior muestra lo que sucede cuando giramos el marco de coordenadas alrededor del eje Z.
La rotación no da lugar a un desplazamiento uniforme, por lo que el vector p mantiene su valor por defecto. Ahora las cosas se ponen un poco más complicadas. Las rotaciones causan que el movimiento a lo largo de cierto eje en el sistema de coordenadas original se mueva en una dirección diferente. Por lo tanto, si giramos un sistema de coordenadas 45 grados alrededor del eje Z, moviéndonos a lo largo del eje x del sistema de coordenadas original, se produce un movimiento en una dirección diagonal entre el eje x y el eje y en el nuevo sistema de coordenadas.
Para simplificar las cosas, le mostraremos cómo las matrices de transformación buscan rotaciones alrededor de los ejes principales.
Around X:
1 0 0 0
0 cos(phi) sin(phi) 0
0 -sin(phi) cos(phi) 0
0 0 0 1
Around Y:
cos(phi) 0 sin(phi) 0
0 1 0 0
-sin(phi) 0 cos(phi) 0
0 0 0 1
Around Z:
cos(phi) -sin(phi) 0 0
sin(phi) cos(phi) 0 0
0 0 1 0
0 0 0 1
Implementación
Todo esto se puede implementar como una clase que almacena 16 números, almacenando matrices en un orden de columna mayor.
function Transformation () {
// Create an identity transformation
this.fields = [1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1]
}
// Multiply matrices, to chain transformations
Transformation.prototype.mult = function (t) {
var output = new Transformation()
for (var row = 0; row < 4; ++row) {
for (var col = 0; col < 4; ++col) {
var sum = 0
for (var k = 0; k < 4; ++k) {
sum += this.fields[k * 4 + row] * t.fields[col * 4 + k]
}
output.fields[col * 4 + row] = sum
}
}
return output
}
// Multiply by translation matrix
Transformation.prototype.translate = function (x, y, z) {
var mat = new Transformation()
mat.fields[12] = Number(x) || 0
mat.fields[13] = Number(y) || 0
mat.fields[14] = Number(z) || 0
return this.mult(mat)
}
// Multiply by scaling matrix
Transformation.prototype.scale = function (x, y, z) {
var mat = new Transformation()
mat.fields[0] = Number(x) || 0
mat.fields[5] = Number(y) || 0
mat.fields[10] = Number(z) || 0
return this.mult(mat)
}
// Multiply by rotation matrix around X axis
Transformation.prototype.rotateX = function (angle) {
angle = Number(angle) || 0
var c = Math.cos(angle)
var s = Math.sin(angle)
var mat = new Transformation()
mat.fields[5] = c
mat.fields[10] = c
mat.fields[9] = -s
mat.fields[6] = s
return this.mult(mat)
}
// Multiply by rotation matrix around Y axis
Transformation.prototype.rotateY = function (angle) {
angle = Number(angle) || 0
var c = Math.cos(angle)
var s = Math.sin(angle)
var mat = new Transformation()
mat.fields[0] = c
mat.fields[10] = c
mat.fields[2] = -s
mat.fields[8] = s
return this.mult(mat)
}
// Multiply by rotation matrix around Z axis
Transformation.prototype.rotateZ = function (angle) {
angle = Number(angle) || 0
var c = Math.cos(angle)
var s = Math.sin(angle)
var mat = new Transformation()
mat.fields[0] = c
mat.fields[5] = c
mat.fields[4] = -s
mat.fields[1] = s
return this.mult(mat)
}
Mira a Través de una Cámara
Aquí viene la parte clave de la presentación de objetos en la pantalla: la cámara. Hay dos componentes clave para una cámara; Su posición, y cómo proyecta objetos observados en la pantalla.
La posición de la cámara se maneja con un simple truco. No hay diferencia visual entre mover la cámara un metro adelante y mover el mundo entero un metro hacia atrás. Así que naturalmente, hacemos esto último aplicando la inversa de la matriz como una transformación.
El segundo componente clave es la forma en que los objetos observados se proyectan sobre el lente. En WebGL, todo lo visible en la pantalla se encuentra en una caja. La caja se extiende entre -1 y 1 en cada eje. Todo lo visible está dentro de esa caja. Podemos utilizar el mismo enfoque de matrices de transformación para crear una matriz de proyección.
Proyección Ortográfica
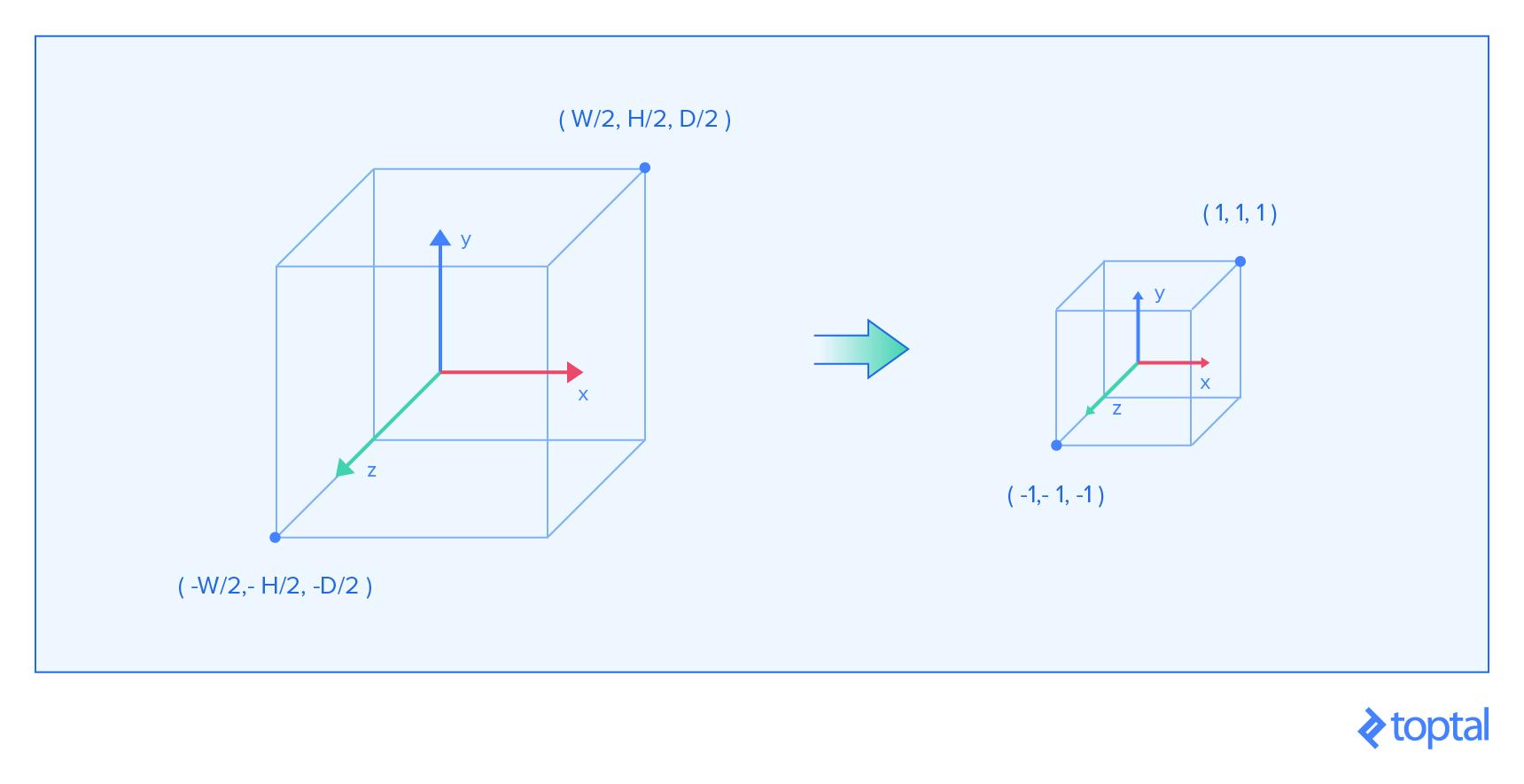
La proyección más simple es la [proyección ortográfica] (https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographical-projection-matrix/orthographic-projection-matrix). Se toma una caja en el espacio que indica el ancho, la altura y la profundidad con la suposición de que su centro está en la posición cero. A continuación, la proyección redimensiona la caja para que se ajuste a la caja previamente descrita dentro de la cual WebGL observa objetos. Dado que queremos cambiar el tamaño de cada dimensión a dos, ajustamos cada eje a 2/size, donde size es la dimensión del eje respectivo. Una pequeña advertencia es el hecho de que estamos multiplicando el eje Z con un negativo. Esto se hace porque queremos voltear la dirección de esa dimensión. La matriz final tiene esta forma:
2/width 0 0 0
0 2/height 0 0
0 0 -2/depth 0
0 0 0 1
Proyección Perspectiva
No vamos a pasar por los detalles de cómo se diseña esta proyección, pero sólo usa la fórmula final, que es bastante estándar por ahora. Podemos simplificarlo colocando la proyección en la posición cero en los ejes x e y, haciendo los límites derecho/izquierdo y superior/inferior iguales a width/2 y height/2, respectivamente. Los parámetros n y f representan los planos de recorte near y far, que son la distancia más pequeña y más grande que un punto puede ser para poder ser capturado por la cámara. Están representados por los lados paralelos del frustum en la imagen anterior.
Una proyección de perspectiva suele estar representada con un campo de visión (we’ll use the vertical one), relación de aspecto, y las distancias de plano cercano y lejano. Esa información se puede utilizar para calcular width y height, y entonces la matriz se puede crear a partir de la siguiente plantilla:
2*n/width 0 0 0
0 2*n/height 0 0
0 0 (f+n)/(n-f) 2*f*n/(n-f)
0 0 -1 0
Para calcular el ancho y la altura, se pueden usar las siguientes fórmulas:
height = 2 * near * Math.tan(fov * Math.PI / 360)
width = aspectRatio * height
El FOV (campo de visión) representa el ángulo vertical que la cámara captura con su lente. La relación de aspecto representa la relación entre el ancho y la altura de la imagen y se basa en las dimensiones de la pantalla que estamos mostrando.
Implementación
Ahora podemos representar una cámara como una clase, la cual almacena la posición de la cámara y la matriz de proyección. También necesitamos saber cómo calcular las transformaciones inversas. Resolver las inversiones de matriz generales puede ser problemático, pero existe un enfoque simplificado para nuestro caso en especial.
function Camera () {
this.position = new Transformation()
this.projection = new Transformation()
}
Camera.prototype.setOrthographic = function (width, height, depth) {
this.projection = new Transformation()
this.projection.fields[0] = 2 / width
this.projection.fields[5] = 2 / height
this.projection.fields[10] = -2 / depth
}
Camera.prototype.setPerspective = function (verticalFov, aspectRatio, near, far) {
var height_div_2n = Math.tan(verticalFov * Math.PI / 360)
var width_div_2n = aspectRatio * height_div_2n
this.projection = new Transformation()
this.projection.fields[0] = 1 / height_div_2n
this.projection.fields[5] = 1 / width_div_2n
this.projection.fields[10] = (far + near) / (near - far)
this.projection.fields[10] = -1
this.projection.fields[14] = 2 * far * near / (near - far)
this.projection.fields[15] = 0
}
Camera.prototype.getInversePosition = function () {
var orig = this.position.fields
var dest = new Transformation()
var x = orig[12]
var y = orig[13]
var z = orig[14]
// Transpose the rotation matrix
for (var i = 0; i < 3; ++i) {
for (var j = 0; j < 3; ++j) {
dest.fields[i * 4 + j] = orig[i + j * 4]
}
}
// Translation by -p will apply R^T, which is equal to R^-1
return dest.translate(-x, -y, -z)
}
Esta es la pieza final que necesitamos antes de que podamos empezar a dibujar en la pantalla.
Dibujar un objeto con el canal de Gráficos WebGL
La superficie más simple que puedes dibujar es un triángulo. De hecho, la mayoría de las cosas que dibujas en el espacio 3D consisten en un gran número de triángulos.
Lo primero que debes entender es cómo se representa la pantalla en WebGL. Es un espacio 3D, que abarca entre -1 y 1 en el eje x, y y z. De forma predeterminada, este eje z no se utiliza, pero estás interesado en gráficos 3D, por lo que deberás habilitarlo de inmediato.
Teniendo esto en cuenta, lo que sigue son tres pasos necesarios para dibujar un triángulo sobre esta superficie.
Puedes definir tres vértices que representarían el triángulo que deseas dibujar. Los datos se serializan y se envían a la GPU (unidad de procesamiento gráfico). Con un modelo entero disponible, puedes hacer eso para todos los triángulos en el modelo. Las posiciones de vértice que das están en el espacio de coordenadas local del modelo que cargaste. Puesto de manera más simple, las posiciones que proporcionas son las exactas del archivo y no las que consigues después de realizar transformaciones de la matriz.
Ahora que le has dado los vértices a la GPU, le dices a la GPU qué lógica usar cuando colocas los vértices en la pantalla. Este paso se utilizará para aplicar nuestras transformaciones de matriz. La GPU es muy buena para multiplicar muchas matrices 4×4, por lo que pondremos esa característica a buen uso.
En el último paso, la GPU rasterizará ese triángulo. La rasterización es el proceso de tomar gráficos vectoriales y determinar qué píxeles de la pantalla necesitan ser pintados, para que el objeto gráfico vectorial se muestre. En nuestro caso, la GPU está tratando de determinar qué píxeles se encuentran dentro de cada triángulo. Para cada píxel, la GPU te preguntará de qué color deseas que esté pintado.
Estos son los cuatro elementos necesarios para dibujar lo que quieras y son el ejemplo más simple de un canal de gráficos. Lo que sigue es una mirada a cada uno de ellos y una implementación simple.
El Framebuffer Predeterminado
El elemento más importante para una aplicación WebGL es el contexto WebGL. Puedes acceder a éste con gl = canvas.getContext ('webgl'), o usar ’experimental-webgl' como alternativa, en caso de que el navegador utilizado actualmente no soporte todas las funciones de WebGL. El ‘lienzo’ al que nos referimos es el elemento DOM del lienzo en el que queremos dibujar. El contexto contiene muchas cosas, entre las cuales está el framebuffer predeterminado.
Podría describir un framebuffer como cualquier buffer (objeto) en el que puedas dibujar. De forma predeterminada, el framebuffer predeterminado almacena el color de cada píxel del lienzo al que está vinculado el contexto de WebGL. Como se describe en la sección anterior, cuando dibujamos sobre el framebuffer, cada píxel está situado entre -1 y 1 en el eje x y y. Algo que también mencionamos es el hecho de que, por defecto, WebGL no utiliza el eje z. Esa funcionalidad se puede habilitar al ejecutar gl.enable (gl.DEPTH_TEST). Genial, pero ¿qué es una prueba de profundidad?
Habilitar la prueba de profundidad permite que un píxel almacene tanto el color como la profundidad. La profundidad es la coordenada z de ese píxel. Después de dibujar un píxel a una cierta profundidad z, para actualizar el color de ese píxel debes dibujar en una posición z que esté más cerca de la cámara. De lo contrario, el intento de dibujo será ignorado. Esto permite la ilusión de 3D ya que dibujar objetos que están detrás de otros objetos hará que los objetos sean ocluidos por otros objetos delante de ellos.
Cualquier dibujo que realices permanecerá en la pantalla hasta que les digas que se despejen. Para ello, tienes que llamar a gl.clear (gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT). Esto borra tanto el color como el buffer de profundidad. Para elegir el color al cual se ajustan los píxeles borrados, usa gl.clearColor (rojo, verde, azul, alfa).
Vamos a crear un procesador que utiliza un lienzo y lo borra a petición:
function Renderer (canvas) {
var gl = canvas.getContext('webgl') || canvas.getContext('experimental-webgl')
gl.enable(gl.DEPTH_TEST)
this.gl = gl
}
Renderer.prototype.setClearColor = function (red, green, blue) {
gl.clearColor(red / 255, green / 255, blue / 255, 1)
}
Renderer.prototype.getContext = function () {
return this.gl
}
Renderer.prototype.render = function () {
this.gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT)
}
var renderer = new Renderer(document.getElementById('webgl-canvas'))
renderer.setClearColor(100, 149, 237)
loop()
function loop () {
renderer.render()
requestAnimationFrame(loop)
}
Adjuntar esta secuencia de comandos al siguiente HTML dará un rectángulo azul brillante en la pantalla
<!DOCTYPE html>
<html>
<head>
</head>
<body>
<canvas id="webgl-canvas" width="800" height="500"></canvas>
<script src="script.js"></script>
</body>
</html>
El llamado requestAnimationFrame hace que el nudo sea llamado nuevamente tan pronto como se haya hecho el renderizado anterior y se haya terminado todo el manejo del evento.
Objetos de Vértices Buffer
Lo primero que debes hacer es definir los vértices que deseas dibujar. Puedes hacer esto describiéndolos a través de vectores en el espacio 3D. Después de eso, debes mover esos datos a la memoria RAM de la GPU, creando un nuevo Buffer Vertex Buffer (VBO).
Un Objeto Buffer en general es un objeto que almacena una matriz de fragmentos de memoria en la GPU. Al ser un VBO, éste sólo denota para lo que la GPU puede utilizar la memoria. La mayoría de las veces, los objetos de buffer que crees serán VBOs.
Puedes llenar el VBO tomando todos los vértices N que tenemos y creando una matriz de floats con elementos 3N para la posición de vértice y VBOs normales de vértice, y 2N para las coordenadas de textura VBO. Cada grupo de tres floats, o dos floats para coordenadas UV, representa coordenadas individuales de un vértice. Luego pasamos estas matrices a la GPU, y nuestros vértices están listos para el resto del canal.
Dado que la data está ahora en la RAM de la GPU, puedes eliminarla de la memoria RAM de uso general. Es decir, a menos que desees modificarla más tarde y volver a cargarla. Cada modificación debe ser seguida por una subida ya que las modificaciones en nuestras matrices JS no se aplican a VBOs en la memoria RAM real de la GPU.
A continuación se muestra un ejemplo de código, el cual proporciona toda la funcionalidad descrita. Una nota importante es el hecho de que las variables almacenadas en la GPU no son recolectadas de la basura. Eso significa que tenemos que eliminarlas manualmente, una vez que no queremos usarlas más. Sólo te daremos un ejemplo de cómo se hace aquí y no nos centrará más en ese concepto. La supresión de variables de la GPU sólo es necesaria si piensa dejar de usar cierta geometría en todo el programa.
También añadimos serialización a nuestra clase Geometry y elementos dentro de ella.
Geometry.prototype.vertexCount = function () {
return this.faces.length * 3
}
Geometry.prototype.positions = function () {
var answer = []
this.faces.forEach(function (face) {
face.vertices.forEach(function (vertex) {
var v = vertex.position
answer.push(v.x, v.y, v.z)
})
})
return answer
}
Geometry.prototype.normals = function () {
var answer = []
this.faces.forEach(function (face) {
face.vertices.forEach(function (vertex) {
var v = vertex.normal
answer.push(v.x, v.y, v.z)
})
})
return answer
}
Geometry.prototype.uvs = function () {
var answer = []
this.faces.forEach(function (face) {
face.vertices.forEach(function (vertex) {
var v = vertex.uv
answer.push(v.x, v.y)
})
})
return answer
}
////////////////////////////////
function VBO (gl, data, count) {
// Creates buffer object in GPU RAM where we can store anything
var bufferObject = gl.createBuffer()
// Tell which buffer object we want to operate on as a VBO
gl.bindBuffer(gl.ARRAY_BUFFER, bufferObject)
// Write the data, and set the flag to optimize
// for rare changes to the data we're writing
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(data), gl.STATIC_DRAW)
this.gl = gl
this.size = data.length / count
this.count = count
this.data = bufferObject
}
VBO.prototype.destroy = function () {
// Free memory that is occupied by our buffer object
this.gl.deleteBuffer(this.data)
}
El tipo de datos VBO genera el VBO en el contexto WebGL pasado, basado en la matriz pasada como segundo parámetro.
Puedes ver tres llamadas al contexto gl. La llamada createBuffer () crea el buffer. La llamada bindBuffer () indica a la máquina de estado WebGL que utilice esta memoria específica como la actual VBO (ARRAY_BUFFER) para todas las operaciones futuras, hasta que se indique lo contrario. Después de eso, establecemos el valor de la VBO actual a los datos proporcionados, con bufferData ().
También proporcionamos un método de destrucción que elimina nuestro objeto de memoria intermedia de la GPU RAM, usando deleteBuffer().
Puedes utilizar tres VBOs y una transformación para describir todas las propiedades de una malla, junto a su posición.
function Mesh (gl, geometry) {
var vertexCount = geometry.vertexCount()
this.positions = new VBO(gl, geometry.positions(), vertexCount)
this.normals = new VBO(gl, geometry.normals(), vertexCount)
this.uvs = new VBO(gl, geometry.uvs(), vertexCount)
this.vertexCount = vertexCount
this.position = new Transformation()
this.gl = gl
}
Mesh.prototype.destroy = function () {
this.positions.destroy()
this.normals.destroy()
this.uvs.destroy()
}
Como ejemplo, aquí se ve cómo podemos cargar un modelo, almacenar sus propiedades en la malla (mesh) y luego destruirlo:
Geometry.loadOBJ('/assets/model.obj').then(function (geometry) {
var mesh = new Mesh(gl, geometry)
console.log(mesh)
mesh.destroy()
})
Shaders
Lo que sigue es el proceso de dos pasos previamente descrito, que se trata de mover puntos en las posiciones deseadas y pintar todos los píxeles individuales. Para ello, escribimos un programa que se ejecuta en la tarjeta gráfica muchas veces. Este programa normalmente consta de al menos dos partes. La primera parte es un Shader de Vértices, que se ejecuta para cada vértice, y las salidas donde debemos colocar el vértice en la pantalla, entre otras cosas. La segunda parte es el Fragmento de Shader, que se ejecuta para cada píxel que cubre un triángulo en la pantalla, y produce el color en el cual el píxel debe ser pintado.
Shaders de Vértices
Digamos que quieres tener un modelo que se mueve de izquierda y derecha en la pantalla. En un enfoque ingenuo, puedes actualizar la posición de cada vértice y volver a enviarlo a la GPU. Ese proceso es costoso y lento. Alternativamente, darías un programa para que la GPU se ejecute para cada vértice y hacer todas esas operaciones en paralelo con un procesador que está construido para hacer exactamente ese trabajo. Ése es el papel de un shader de vértices.
Un shader de vértices es la parte de la canalización de procesamiento que procesa vértices individuales. Una llamada al shader de vértices recibe un único vértice y genera un único vértice después de aplicar todas las transformaciones posibles al vértice.
Shaders están escritos en GLSL. Hay muchos elementos únicos en este lenguaje, pero la mayoría de la sintaxis es muy similar a C, por lo que debe ser comprensible para la mayoría de las personas.
Hay tres tipos de variables que entran y salen de un shader de vértices, y todas ellas sirven a un uso específico:
atributo— Estas son entradas que contienen propiedades específicas de un vértice. Anteriormente describimos la posición de un vértice como un atributo en forma de un vector de tres elementos. Puedes ver a los atributos como valores que describen un vértice.uniforme— Estas son entradas que son las mismas para cada vértice dentro de la misma llamada de renderizado. Digamos que queremos mover nuestro modelo, definiendo una matriz de transformación. Puedes usar una variableuniformepara describir eso. También puedes usar recursos de la GPU, como texturas. Puedes ver estos uniformes como valores que describen un modelo o una parte de un modelo.variaciones— Estas son las salidas que pasamos al fragmento de shader. Puesto que hay potencialmente miles de píxeles para un triángulo de vértices, cada píxel recibirá un valor interpolado para esta variable, dependiendo de la posición. Así que si un vértice envía 500 como una salida, y en otro 100, un píxel que está en el medio de estos recibirá 300 como entrada para esa variable. Puedes ver las variaciones como valores que describen superficies entre vértices.
Por lo tanto, digamos que deseas crear un shader de vértices que reciba una posición normal y coordenadas uv para cada vértice, y una posición vista (posición de cámara inversa) y una matriz de proyección para cada objeto representado. Digamos que también quieres pintar píxeles individuales basados en sus coordenadas uv y sus normales. Te preguntarás “¿Cómo se vería ese código?”.
attribute vec3 position;
attribute vec3 normal;
attribute vec2 uv;
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;
varying vec3 vNormal;
varying vec2 vUv;
void main() {
vUv = uv;
vNormal = (model * vec4(normal, 0.)).xyz;
gl_Position = projection * view * model * vec4(position, 1.);
}
La mayoría de estos elementos deben ser auto-explicativos. Lo más importante es notar que no hay valores de retorno en la función main. Todos los valores que quisiéramos retornar se asignan, ya sea a variables variantes o a variables especiales. Aquí asignamos a gl_Position, que es un vector de cuatro dimensiones, por lo que la última dimensión siempre debe estar en uno. Otra cosa extraña que podrías notar es la forma en que construimos un vec4 fuera del vector de posición. Puedes construir un vec4 usando cuatro floats, dos vec2s, o cualquier otra combinación que resulte en cuatro elementos. Hay un muchos tipos de castings, aparentemente, extraños que tienen sentido una vez que estés familiarizado con las matrices de transformación.
También puedes ver que aquí podemos realizar transformaciones de matriz fácilmente. GLSL está específicamente diseñado para este tipo de trabajo. La posición de salida se calcula multiplicando la proyección, la vista y la matriz del modelo y aplicándola a la posición. La salida normal se acaba de transformar en el espacio mundial. Más adelante explicaremos por qué nos hemos detenido allí con las transformaciones normales.
Por ahora, lo mantendremos sencillo y pasaremos a pintar píxeles individuales.
Fragmento de Shaders
Un fragmento shader es el paso después de la rasterización en el canal de gráficos. Genera color, profundidad y otros datos para cada píxel del objeto que se está pintando
Los principios detrás de la implementación de shaders de fragmentos son muy similares a los shaders de vértices. Sin embargo, hay tres grandes diferencias:
- No hay más salidas
variables, y las entradasatributoshan sido reemplazadas con entradas `variadas’. Acabamos de pasar a nuestro canal, y las cosas que son la salida en el shader vértice son ahora entradas en el fragmento de shader. - Nuestra única salida ahora es
gl_FragColor, que es unvec4. Los elementos representan rojo, verde, azul y alfa (RGBA), respectivamente, con variables en el rango de 0 a 1. Debes mantener alfa en 1, a menos que estés haciendo la transparencia. Sin embargo, la transparencia es un concepto bastante avanzado, por lo que nos atenemos a los objetos opacos. - Al principio del fragmento de shader, es necesario establecer la precisión del flotador, que es importante para las interpolaciones. En casi todos los casos, sólo se adhieren a las líneas del siguiente shader.
Con esto en mente, puedes escribir fácilmente un shader que pinta el canal rojo basado en la posición U, canal verde basado en la posición V, y fija el canal azul al máximo.
#ifdef GL_ES
precision highp float;
#endif
varying vec3 vNormal;
varying vec2 vUv;
void main() {
vec2 clampedUv = clamp(vUv, 0., 1.);
gl_FragColor = vec4(clampedUv, 1., 1.);
}
La función clamp sólo limita todos los floats en un objeto para estar dentro de los límites dados. El resto del código debe ser bastante sencillo.
Con todo esto en mente, lo que queda por hacer es implementar esto en WebGL.
Combinación de Shaders en un Programa
El siguiente paso es combinar los shaders en un programa:
function ShaderProgram (gl, vertSrc, fragSrc) {
var vert = gl.createShader(gl.VERTEX_SHADER)
gl.shaderSource(vert, vertSrc)
gl.compileShader(vert)
if (!gl.getShaderParameter(vert, gl.COMPILE_STATUS)) {
console.error(gl.getShaderInfoLog(vert))
throw new Error('Failed to compile shader')
}
var frag = gl.createShader(gl.FRAGMENT_SHADER)
gl.shaderSource(frag, fragSrc)
gl.compileShader(frag)
if (!gl.getShaderParameter(frag, gl.COMPILE_STATUS)) {
console.error(gl.getShaderInfoLog(frag))
throw new Error('Failed to compile shader')
}
var program = gl.createProgram()
gl.attachShader(program, vert)
gl.attachShader(program, frag)
gl.linkProgram(program)
if (!gl.getProgramParameter(program, gl.LINK_STATUS)) {
console.error(gl.getProgramInfoLog(program))
throw new Error('Failed to link program')
}
this.gl = gl
this.position = gl.getAttribLocation(program, 'position')
this.normal = gl.getAttribLocation(program, 'normal')
this.uv = gl.getAttribLocation(program, 'uv')
this.model = gl.getUniformLocation(program, 'model')
this.view = gl.getUniformLocation(program, 'view')
this.projection = gl.getUniformLocation(program, 'projection')
this.vert = vert
this.frag = frag
this.program = program
}
// Loads shader files from the given URLs, and returns a program as a promise
ShaderProgram.load = function (gl, vertUrl, fragUrl) {
return Promise.all([loadFile(vertUrl), loadFile(fragUrl)]).then(function (files) {
return new ShaderProgram(gl, files[0], files[1])
})
function loadFile (url) {
return new Promise(function (resolve) {
var xhr = new XMLHttpRequest()
xhr.onreadystatechange = function () {
if (xhr.readyState == XMLHttpRequest.DONE) {
resolve(xhr.responseText)
}
}
xhr.open('GET', url, true)
xhr.send(null)
})
}
}
No hay mucho que decir sobre lo que está sucediendo aquí. A cada shader se le asigna una cadena como fuente y se compila, después de lo cual verificamos si hay errores de compilación. Entonces, creamos un programa enlazando estos dos shaders. Finalmente, almacenamos punteros para todos los atributos y uniformes relevantes para la posteridad.
Realmente dibujando el modelo
Por último, pero no menos importante, dibuja el modelo.
Primero escoge el programa de shader que deseas usar
ShaderProgram.prototype.use = function () {
this.gl.useProgram(this.program)
}
A continuación, envía todos los uniformes relacionados con la cámara a la GPU. Estos uniformes cambian sólo una vez por cada cambio de cámara o movimiento.
Transformation.prototype.sendToGpu = function (gl, uniform, transpose) {
gl.uniformMatrix4fv(uniform, transpose || false, new Float32Array(this.fields))
}
Camera.prototype.use = function (shaderProgram) {
this.projection.sendToGpu(shaderProgram.gl, shaderProgram.projection)
this.getInversePosition().sendToGpu(shaderProgram.gl, shaderProgram.view)
}
Por último, se toman las transformaciones y VBOs y se asignan a uniformes y atributos, respectivamente. Dado que esto tiene que hacerse a cada VBO, puede crear su vinculación de datos como un método.
VBO.prototype.bindToAttribute = function (attribute) {
var gl = this.gl
// Tell which buffer object we want to operate on as a VBO
gl.bindBuffer(gl.ARRAY_BUFFER, this.data)
// Enable this attribute in the shader
gl.enableVertexAttribArray(attribute)
// Define format of the attribute array. Must match parameters in shader
gl.vertexAttribPointer(attribute, this.size, gl.FLOAT, false, 0, 0)
}
A continuación, se asigna una matriz de tres floats para el uniforme. Cada tipo de uniforme tiene una firma diferente, por lo que la documentación y más documentación son tus amigos aquí. Finalmente, dibuja la matriz triangular en la pantalla. Le dice a la llamada de dibujo [drawArrays ()] (https://developer.mozilla.org/en-US/docs/Web/API/WebGLRenderingContext/drawArrays) desde que vértice puede iniciar, y cuántos vértices dibujar. El primer parámetro pasado le dice a WebGL cómo interpretará la matriz de vértices. El uso de TRIÁNGULOS toma tres por tres vértices y dibuja un triángulo para cada triplete. Usar PUNTOS sólo dibujaría un punto para cada vértice pasado. Hay muchas más opciones, pero no hay necesidad de descubrir todo al mismo tiempo. A continuación se muestra el código para dibujar un objeto:
Mesh.prototype.draw = function (shaderProgram) {
this.positions.bindToAttribute(shaderProgram.position)
this.normals.bindToAttribute(shaderProgram.normal)
this.uvs.bindToAttribute(shaderProgram.uv)
this.position.sendToGpu(this.gl, shaderProgram.model)
this.gl.drawArrays(this.gl.TRIANGLES, 0, this.vertexCount)
}
El renderizador necesita ser extendido un poco, para acomodar todos los elementos adicionales que necesitan ser manejados. Debe ser posible adjuntar un programa de shader y renderizar una matriz de objetos basada en la posición actual de la cámara.
Renderer.prototype.setShader = function (shader) {
this.shader = shader
}
Renderer.prototype.render = function (camera, objects) {
this.gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT)
var shader = this.shader
if (!shader) {
return
}
shader.use()
camera.use(shader)
objects.forEach(function (mesh) {
mesh.draw(shader)
})
}
Podemos combinar todos los elementos que tenemos para finalmente dibujar algo en la pantalla:
var renderer = new Renderer(document.getElementById('webgl-canvas'))
renderer.setClearColor(100, 149, 237)
var gl = renderer.getContext()
var objects = []
Geometry.loadOBJ('/assets/sphere.obj').then(function (data) {
objects.push(new Mesh(gl, data))
})
ShaderProgram.load(gl, '/shaders/basic.vert', '/shaders/basic.frag')
.then(function (shader) {
renderer.setShader(shader)
})
var camera = new Camera()
camera.setOrthographic(16, 10, 10)
loop()
function loop () {
renderer.render(camera, objects)
requestAnimationFrame(loop)
}
Esto parece un poco aleatorio, pero se puede ver los diferentes parches de la esfera, en función de dónde están en el mapa UV. Puedes cambiar el shader para pintar el objeto marrón. Simplemente establece el color para cada píxel para que sea el RGBA para marrón:#ifdef GL_ES
precision highp float;
#endif
varying vec3 vNormal;
varying vec2 vUv;
void main() {
vec3 brown = vec3(.54, .27, .07);
gl_FragColor = vec4(brown, 1.);
}
No parece muy convincente. Parece que la escena necesita algunos efectos de sombreado.
Añadiendo luz
Las luces y las sombras son las herramientas que nos permiten percibir la forma de los objetos. Las luces vienen en muchas formas y tamaños: focos que brillan en un cono, bombillas que difunden luz en todas direcciones, y lo más interesante, el sol, que está tan lejos que toda la luz que brilla sobre nosotros irradia, para todos los intentos y en la misma dirección.
La luz solar suena como si fuera la más sencilla de implementar ya que todo lo que necesita proporcionar es la dirección en la que se propagan todos los rayos. Para cada píxel que dibujes en la pantalla, comprueba el ángulo bajo el cual la luz golpea el objeto. Aquí es donde entran las normales de superficie.
A Dónde ir Después
Hay muchas fuentes de información para aprender todos los trucos y complejidades de WebGL. Y la mejor parte es que si no puedes encontrar una respuesta relacionada con WebGL, puedes buscarla en OpenGL, ya que WebGL se basa en un subconjunto de OpenGL con algunos nombres cambiados.
En ningún orden en particular, aquí hay algunas fuentes excelentes para obtener información más detallada, tanto para WebGL como para OpenGL.
- Fundamentos de WebGL
- WebGL de aprendizaje
- Un tutorial muy detallado OpenGL tutorial, te guiará a través de todos los principios fundamentales descritos aquí, de una manera muy lenta y detallada.
- Y hay muchos, muchos otros sitios dedicados a enseñarte los principios de la computación gráfica.
- Documentación de MDN para WebGL
- Especificación de Khronos WebGL 1.0 si estás interesado en comprender los detalles más técnicos de cómo debería funcionar la API WebGL en todos los casos.
Artículo Vía Toptal




